If $A B$ is a chord of length $5 \sqrt{3} \mathrm{~cm}$ of a circle with centre $O$ and radius $5 \mathrm{~cm}$, then area of sector $O A B$ is
(a) $\frac{3 \pi}{8} \mathrm{~cm}^{2}$
(b) $\frac{8 \pi}{3} \mathrm{~cm}^{2}$
(c) $25 \pi \mathrm{cm}^{2}$
(d) $\frac{25 \pi}{3} \mathrm{~cm}^{2}$
We have to find the area of the sector OAB.
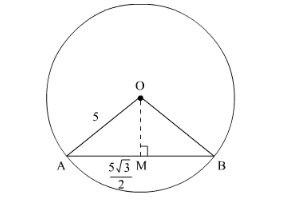
We have,
$\mathrm{AM}=\frac{5 \sqrt{3}}{2}$
So,
$\sin \angle \mathrm{AOM}=\frac{5 \sqrt{3}}{2(5)}$
Hence,
$\angle \mathrm{AOM}=60^{\circ}$
Therefore area of the sector,
$=\frac{1}{2} r^{2} \theta$
$=\frac{1}{2}(25)\left(\frac{2 \pi}{3}\right)$
$=\frac{25 \pi}{3} \mathrm{~cm}^{2}$
So answer is (d)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.