If a tangent to the ellipse $x^{2}+4 y^{2}=4$ meets the tangents at the extremities of its major axis at B and $\mathrm{C}$, then the circle with $\mathrm{BC}$ as diameter passes through the point :
Correct Option: 1
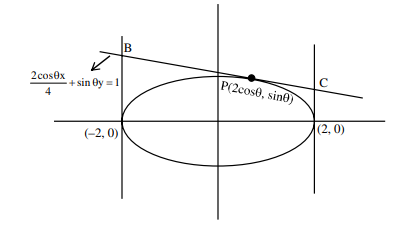
$\frac{x^{2}}{4}+\frac{y^{2}}{1}=1$
Equation of tangent is $(\cos \theta) x+2 \sin \theta y=2$
$\mathrm{B}\left(-2, \frac{1+\cos \theta}{\sin \theta}\right), \quad \mathrm{C}\left(2, \frac{1-\cos \theta}{\sin \theta}\right)$
$\mathrm{B}\left(-2, \cot \frac{\theta}{2}\right) \quad \mathrm{C}\left(2, \tan \frac{\theta}{2}\right)$
Equation of circle is
$(x+2)(x-2)+\left(y-\cot \frac{\theta}{2}\right)\left(y-\tan \frac{\theta}{2}\right)=0$
$x^{2}-4+y^{2}-\left(\tan \frac{\theta}{2}+\cot \frac{\theta}{2}\right) y+1=0$
so, $(\sqrt{3}, 0)$ satisfying option (1)
