If a rectangle is inscribed in an equilateral triangle of side

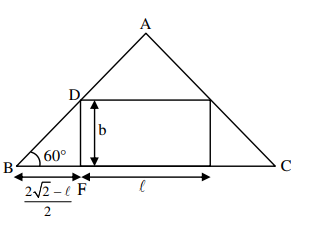
In $\triangle \mathrm{DBF}$

$\tan 60^{\circ}=\frac{2 b}{2 \sqrt{2}-\ell} \Rightarrow b=\frac{\sqrt{3}(2 \sqrt{2}-\ell)}{2}$

$\mathrm{A}=$ Area of rectangle $=\ell \times \mathrm{b}$

$A=\ell \times \frac{\sqrt{3}}{2}(2 \sqrt{2}-\ell)$

$\frac{\mathrm{d} \mathrm{A}}{\mathrm{d} \ell}=\frac{\sqrt{3}}{2}(2 \sqrt{2}-\ell)-\frac{\ell \cdot \sqrt{3}}{2}=0$

$\ell=\sqrt{2}$

$A=\ell \times b=\sqrt{2} \times \frac{\sqrt{3}}{2}(\sqrt{2})=\sqrt{3}$

$\Rightarrow \mathrm{A}^{2}=3$