Question:
If a pair of opposite sides of a cyclic quadrilateral are equal, then prove that its diagonals are also equal.
Thinking Process
Firstly, prove that ΔACD is congruent to ΔBDC by SAS and then further prove the required result
Solution:
Given Let ABCD be a cyclic quadrilateral and AD = BC.
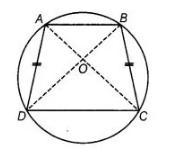
Join AC and BD.
To prove AC = BD
Proof In ΔAOD and ΔBOC,
∠OAD = ∠OBC and ∠ODA = ∠OCB
[since, same segments subtends equal angle to the circle]
AB = BC [given]
ΔAOD = ΔBOC [by ASA congruence rule]
Adding is DOC on both sides, we get
ΔAOD+ ΔDOC ≅ ΔBOC + ΔDOC
=> ΔADC ≅ ΔBCD
AC = BD [by CPCT]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.