If a line segment joining mid-points

Given $A B$ and $C D$ are two chords of a circle whose centre is $O$ and $P Q$ is a diameter bisecting the chord $A B$ and $C D$ at $L$ and $M$, respectively and the diameter $P Q$ passes through the centre $O$ of the circle.

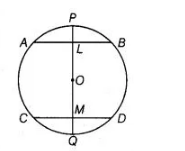
To prove $A B \| C D$

Proof Since, $L$ is the mid-point of $A B$.

$\therefore \quad O L \perp A B$

[since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord]

$\Rightarrow$ $\angle A L O=90^{\circ}$ ...(i)

Similarly, $O M \perp C D$

$\because$ $\angle O M D=90^{\circ}$  .....(ii)

From Eqs. (i) and (ii), $\quad \angle A L O=\angle O M D=90^{\circ}$

But, these are alternating angles.

So,        $A B \| C D$

Hence proved.