If a cone is cut into two parts by a horizontal plane passing through

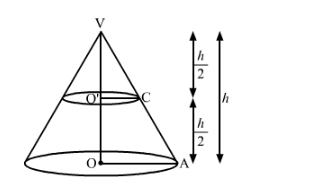
Since,

$\Delta V O A-\Delta V O^{\prime} C$

Therefore,

In $\Delta V O A$ and $\Delta V O^{\prime} C$

$\frac{O^{\prime} V}{O V}=\frac{O^{\prime} C}{O A}$

$\frac{\frac{h}{2}}{h}=\frac{O^{\prime} C}{O A}$

$\frac{1}{2}=\frac{O^{\prime} C}{O A}$

$\frac{O^{\prime} C}{O A}=\frac{1}{2}$

The ratio of the volume of upper part and the cone,

$\frac{V_{1}}{V_{2}}=\frac{\frac{1}{3} \pi\left(O^{\prime} C\right) \times \frac{h}{2}}{\frac{1}{3} \pi(O A)^{2} \times h}$

$\frac{V_{1}}{V_{2}}=\left(\frac{O^{\prime} C}{O A}\right)^{2} \times \frac{1}{2}$............(ii)

From eq. (i) and (ii),

We get,

$\frac{V_{1}}{V_{2}}=\left(\frac{1}{2}\right)^{2} \times \frac{1}{2}$

$\frac{V_{1}}{V_{2}}=\frac{1}{4} \times \frac{1}{2}$

$V_{1}: V_{2}=1: 8$

Hence, the correct answer is choice (d).