Question:
If a circle of radius $R$ passes through the origin $O$ and intersects the coordinate axes at $A$ and $B$, then the locus of the foot of perpendicular from $O$ on $\mathrm{AB}$ is :
Correct Option: , 3
Solution:
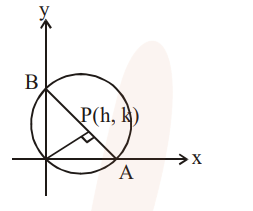
Slope of $\mathrm{AB}=\frac{-\mathrm{h}}{\mathrm{k}}$
Equation of $\mathrm{AB}$ is $\mathrm{hx}+\mathrm{ky}=\mathrm{h}^{2}+\mathrm{k}^{2}$
$\mathrm{A}\left(\frac{\mathrm{h}^{2}+\mathrm{k}^{2}}{\mathrm{~h}}, 0\right), \mathrm{B}\left(0, \frac{\mathrm{h}^{2}+\mathrm{k}^{2}}{\mathrm{k}}\right)$
$\mathrm{AB}=2 \mathrm{R}$
$\Rightarrow\left(h^{2}+k^{2}\right)^{3}=4 R^{2} h^{2} k^{2}$
$\Rightarrow\left(x^{2}+y^{2}\right)^{3}=4 R^{2} x^{2} y^{2}$
