If a circle C passing through the point

The equation of circle $x^{2}+y^{2}+4 x-6 y=12$

can be written as $(x+2)^{2}+(y-3)^{2}=25$

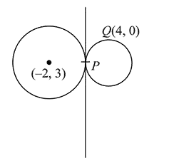
Let $P=(1,-1) \& Q=(4,0)$

Equation of tangent at $P(1,-1)$ to the given circle :

$x(1)+y(-1)+2(x+1)-3(y-1)-12=0$

$3 x-4 y-7=0$$\ldots(1)$

The required circle is tangent to $(1)$ at $(1,-1)$.

$\therefore(x-1)^{2}+(y+1)^{2}+\lambda(3 x-4 y-7)=0$$\ldots(2)$

Equation (2) passes through $Q(4,0)$

$\Rightarrow 3^{2}+1^{2}+\lambda(12-7)=0 \Rightarrow 5 \lambda+10=0$

$\Rightarrow \lambda=-2$

Equation (2) becomes $x^{2}+y^{2}-8 x+10 y+16=0$

radius $=\sqrt{(-4)^{2}+(5)^{2}-16}=5$