Question:
If $\angle \mathrm{A}$ and $\angle \mathrm{B}$ are acute angles such that $\tan \mathrm{A}=\tan \mathrm{B}$, the prove that $\angle \mathrm{A}=\angle \mathrm{B}$.
Solution:
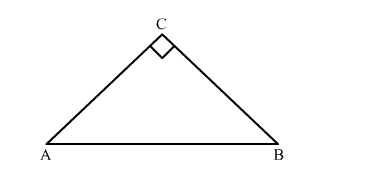
In $\triangle \mathrm{ABC}, \angle \mathrm{C}=90^{\circ}$,
$\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}$ and
$\tan \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}$
As, $\tan \mathrm{A}=\tan \mathrm{B}$
$\Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{AC}}{\mathrm{BC}}$
$\Rightarrow \mathrm{BC}^{2}=\mathrm{AC}^{2}$
$\Rightarrow \mathrm{BC}=\mathrm{AC}$
So, $\angle \mathrm{A}=\angle \mathrm{B} \quad$ (Angles opposite to equal sides are equal)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.