Question:
If $\angle A$ and $\angle B$ are acute angles such that $\sin A=\sin B$, then prove that $\angle A=\angle B$.
Solution:
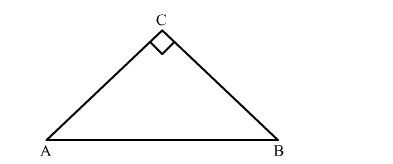
$\ln \triangle \mathrm{ABC}, \angle \mathrm{C}=90^{\circ}$
$\sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}$ and
$\sin B=\frac{A C}{A B}$
As, sinA = sinB
$\Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\mathrm{AC}}{\mathrm{AB}}$
So,
