From the top of a vertical tower, the angles of depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60°.

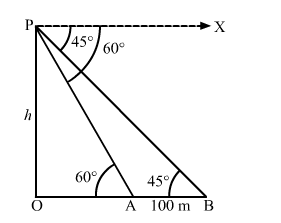
Let OP be the tower and points A and B be the positions of the cars.

We have,

$\mathrm{AB}=100 \mathrm{~m}, \angle \mathrm{OAP}=60^{\circ}$ and $\angle \mathrm{OBP}=45^{\circ}$

Let $\mathrm{OP}=h$

In $\Delta \mathrm{AOP}$,

$\tan 60^{\circ}=\frac{O P}{O A}$

$\Rightarrow \sqrt{3}=\frac{h}{\mathrm{OA}}$

$\Rightarrow \mathrm{OA}=\frac{h}{\sqrt{3}}$

Also, in $\Delta$ BOP,

$\tan 45^{\circ}=\frac{\mathrm{OP}}{\mathrm{OB}}$

$\Rightarrow 1=\frac{h}{\mathrm{OB}}$

$\Rightarrow \mathrm{OB}=h$

Now, OB $-$ OA $=100$

$\Rightarrow h-\frac{h}{\sqrt{3}}=100$

$\Rightarrow \frac{h \sqrt{3}-h}{\sqrt{3}}=100$

$\Rightarrow \frac{h(\sqrt{3}-1)}{\sqrt{3}}=100$

$\Rightarrow h=\frac{100 \sqrt{3}}{(\sqrt{3}-1)} \times \frac{(\sqrt{3}+1)}{(\sqrt{3}+1)}$

$\Rightarrow h=\frac{100 \sqrt{3}(\sqrt{3}+1)}{(3-1)}$

$\Rightarrow h=\frac{100(3+\sqrt{3})}{2}$

$\Rightarrow h=50(3+1.732)$

$\Rightarrow h=50(4.732)$

$\therefore h=236.6 \mathrm{~m}$

So, the height of the tower is 236.6 m.

Disclaimer: The answer given in the texbook is incorrect. The same has been rectified above.