From the top of a tower 100 m high, a man observes two cars on the opposite sides of the tower with angles of depression 30° and 45°, respectively.

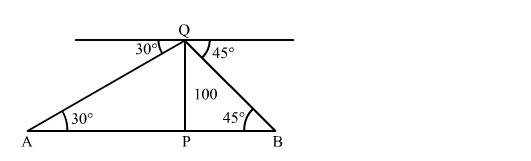
Let PQ be the tower.

We have,

$\mathrm{PQ}=100 \mathrm{~m}, \angle \mathrm{PAQ}=30^{\circ}$ and $\angle \mathrm{PBQ}=45^{\circ}$

In $\Delta \mathrm{APQ}$,

$\tan 30^{\circ}=\frac{\mathrm{PQ}}{\mathrm{AP}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{100}{\mathrm{AP}}$

$\Rightarrow \mathrm{AP}=100 \sqrt{3} \mathrm{~m}$

Als, in $\triangle \mathrm{BPQ}$,

$\tan 45^{\circ}=\frac{\mathrm{PQ}}{\mathrm{BP}}$

$\Rightarrow 1=\frac{100}{\mathrm{BP}}$

$\Rightarrow \mathrm{BP}=100 \mathrm{~m}$

Now, $\mathrm{AB}=\mathrm{AP}+\mathrm{BP}$

$=100 \sqrt{3}+100$

$=100(\sqrt{3}+1)$

$=100 \times(1.73+1)$

$=100 \times 2.73$

$=273 \mathrm{~m}$

So, the distance between the cars is 273 m.