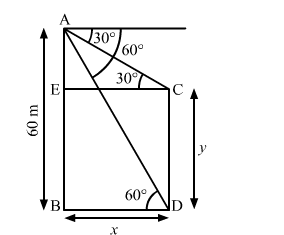
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60°, respectively.

We have,

$\mathrm{AB}=60 \mathrm{~m}, \angle \mathrm{ACE}=30^{\circ}$ and $\angle \mathrm{ADB}=60^{\circ}$

Let $\mathrm{BD}=\mathrm{CE}=x$ and $\mathrm{CD}=\mathrm{BE}=y$

$\Rightarrow \mathrm{AE}=\mathrm{AB}-\mathrm{BE}=60-y$

In $\Delta \mathrm{ACE}$,

$\tan 30^{\circ}=\frac{\mathrm{AE}}{\mathrm{CE}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{60-y}{x}$

$\Rightarrow x=60 \sqrt{3}-y \sqrt{3} \quad \ldots$ (i)

Also, in $\triangle \mathrm{ABD}$,

$\tan 60^{\circ}=\frac{\mathrm{AB}}{\mathrm{BD}}$

$\Rightarrow \sqrt{3}=\frac{60}{x}$

$\Rightarrow x=\frac{60}{\sqrt{3}}$

$\Rightarrow x=\frac{60}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$

$\Rightarrow x=\frac{60 \sqrt{3}}{3}$

$\Rightarrow x=20 \sqrt{3}$

Substituting $x=20 \sqrt{3}$ in (i), we get

$20 \sqrt{3}=60 \sqrt{3}-y \sqrt{3}$

$\Rightarrow y \sqrt{3}=60 \sqrt{3}-20 \sqrt{3}$

$\Rightarrow y \sqrt{3}=40 \sqrt{3}$

$\Rightarrow y=\frac{40 \sqrt{3}}{\sqrt{3}}$

$\Rightarrow y=40 \mathrm{~m}$

(i) the horizontal distance between $\mathrm{AB}$ and $\mathrm{CD}=\mathrm{BD}=x$

$=20 \sqrt{3}$

$=20 \times 1.732$

$=34.64 \mathrm{~m}$

(ii) the height of the lamp post $=\mathrm{CD}=y=40 \mathrm{~m}$

(iii) the difference between the heights of the building and the lamp post $=\mathrm{AB}-\mathrm{CD}=60-40=20 \mathrm{~m}$