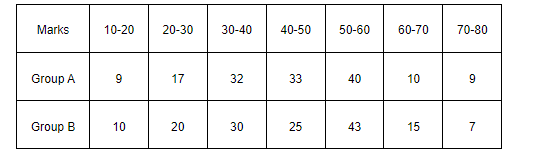
From the data given below state which group is more variable, A or B?

Firstly, the standard deviation of group A is calculated as follows.

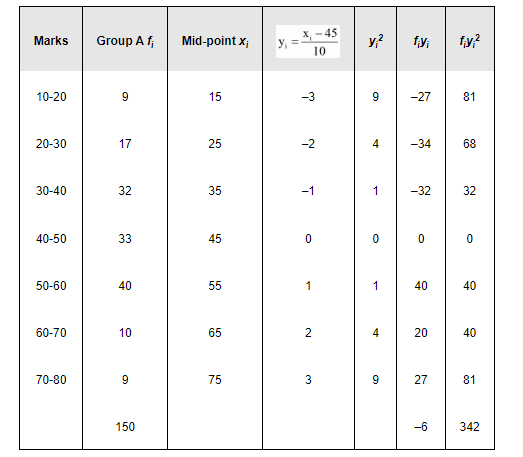
Here, h = 10, N = 150, A = 45

Mean $=\mathrm{A}+\frac{\sum_{\mathrm{i}=1}^{7} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}} \times \mathrm{h}=45+\frac{(-6) \times 10}{150}=45-0.4=44.6$

$\sigma_{1}^{2}=\frac{h^{2}}{N^{2}}\left(N \sum_{i=1}^{7} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{7} f_{i} y_{i}\right)^{2}\right)$

$=\frac{100}{22500}\left(150 \times 342-(-6)^{2}\right)$

$=\frac{1}{225}(51264)$

$=227.84$

$\therefore S \tan$ dard deviation $\left(\sigma_{1}\right)=\sqrt{227.84}=15.09$

The standard deviation of group B is calculated as follows.

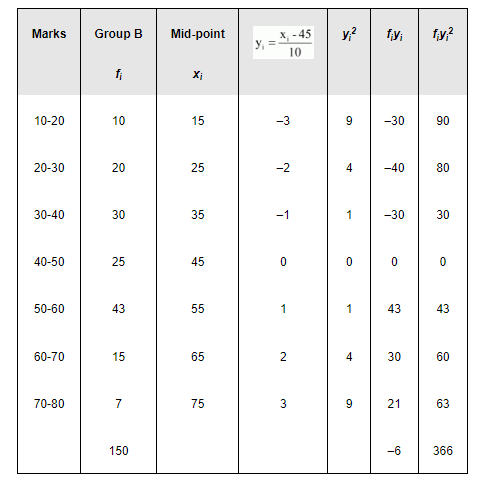
Mean $=\mathrm{A}+\frac{\sum_{\mathrm{i}=1}^{7} \mathrm{f}_{\mathrm{i}} \mathrm{y}_{i}}{\mathrm{~N}} \times \mathrm{h}=45+\frac{(-6) \times 10}{150}=45-0.4=44.6$

$\sigma_{2}^{2}=\frac{h^{2}}{N^{2}}\left[N \sum_{i=1}^{7} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{7} f_{i} y_{i}\right)^{2}\right]$

$=\frac{100}{22500}\left[150 \times 366-(-6)^{2}\right]$

$=\frac{1}{225}[54864]=243.84$

$\therefore$ Stan dard deviation $\left(\sigma_{2}\right)=\sqrt{243.84}=15.61$

Since the mean of both the groups is same, the group with greater standard deviation will be more variable.

Thus, group B has more variability in the marks.