From a uniform disk of radius R, a circular hole of radius R/2 is cut out.

R/6; from the original centre of the body and opposite to the centre of the cut portion.

Mass per unit area of the original disc $=\sigma$

Radius of the original disc $=R$

Mass of the original disc, $M=\pi R^{2} \sigma$

The disc with the cut portion is shown in the following figure:

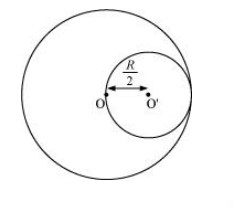
Radius of the smaller disc $=\frac{R}{2}$

Mass of the smaller disc, $M=\pi\left(\frac{R}{2}\right)^{2} \sigma=\frac{1}{4} \pi R^{2} \sigma=\frac{M}{4}$

Let $O$ and $O^{\prime}$ be the respective centres of the original disc and the disc cut off from the original. As per the definition of the centre of mass, the centre of mass of the original disc is supposed to be concentrated at $\mathrm{O}$, while that of the smaller disc is supposed to be concentrated at $O^{\prime}$.

It is given that:

$O O^{\prime}=\frac{R}{2}$

After the smaller disc has been cut from the original, the remaining portion is considered to be a system of two masses. The two masses are:

M (concentrated at O), and

$-M\left(=\frac{M}{4}\right)$ concentrated at $O^{\prime}$

(The negative sign indicates that this portion has been removed from the original disc.)

Let x be the distance through which the centre of mass of the remaining portion shifts from point O.

The relation between the centres of masses of two masses is given as:

$x=\frac{m_{1} r_{1}+m_{2} r_{2}}{m_{1}+m_{2}}$

For the given system, we can write:

$x=\frac{M \times 0-M \times\left(\frac{R}{2}\right)}{M+\left(-M^{\prime}\right)}$

$=\frac{\frac{-M}{4} \times \frac{R}{2}}{M-\frac{M}{4}}=\frac{-M R}{8} \times \frac{4}{3 M}=\frac{-R}{6}$

(The negative sign indicates that the centre of mass gets shifted toward the left of point $O$.)