From a thin metallic piece, in the shape of a trapezium ABCD,

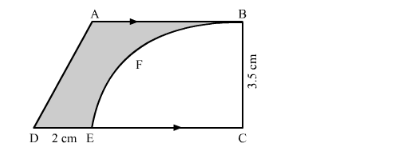
We have given a trapezium. We are asked to find the area of the shaded region.

We can find the area of the remaining part that is area of the shaded region as shown below.

Area of the shaded region $=$ Area of the trapezium $-$ Area of the sector

$\therefore$ Area of the shaded region $=\frac{1}{2}(A B+C D) \times B C-\frac{\theta}{360} \pi r^{2}$

$\therefore$ Area of the shaded region $=\frac{1}{2}(3.5+C D) \times 3.5-\frac{90}{360} \pi(3.5)^{2}$........(1)

Now we find the value of CD.

$C D=C E+D E$

$\therefore C D=3.5+2 \ldots \ldots \ldots$ (Since, $\mathrm{CE}$ is radius of the sector, therefore, $\mathrm{CE}=3.5$ )

$\therefore C D=5.5$

Substituting the values of $\mathrm{CD}$ and $\pi=\frac{22}{7}$ in equation (1),

$\therefore$ Area of the shaded region $=\frac{1}{2}(3.5+5.5) \times 3.5-\frac{90}{360} \times \frac{22}{7} \times(3.5)^{2}$

$\therefore$ Area of the shaded region $=\frac{31.5}{2}-\frac{1}{4} \times 22 \times 0.5 \times 3.5$

$\therefore$ Area of the shaded region $=\frac{31.5}{2}-\frac{19.25}{2}$

$\therefore$ Area of the shaded region $=\frac{12.25}{2}$

$\therefore$ Area of the shaded region $=6.125$

Therefore, area of the remaining part is $6.125 \mathrm{~cm}^{2}$.