From a cubical piece of wood of side 21 cm,

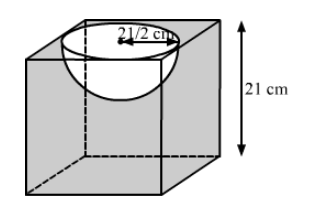
We have,

the edge of the cubical piece, $a=21 \mathrm{~cm}$ and

the radius of the hemisphere, $r=\frac{a}{2}=\frac{21}{2} \mathrm{~cm}$

The surface area of the remaining piece $=$ TSA of cube + CSA of hemisphere - Area of circle

$=6 a^{2}+2 \pi r^{2}-\pi r^{2}$

$=6 a^{2}+\pi r^{2}$

$=6 \times 21 \times 21+\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}$

$=21 \times 21\left(6+\frac{22}{7 \times 4}\right)$

$=21 \times 21\left(6+\frac{11}{14}\right)$

$=21 \times 21\left(\frac{84+11}{14}\right)$

$=21 \times 3\left(\frac{95}{2}\right)$

$=2992.5 \mathrm{~cm}^{2}$

Also,

Volume of the remaining piece $=$ Volume of the cube $-$ Volume of the hemisphere

$=a^{3}-\frac{2}{3} \pi r^{3}$

$=21 \times 21 \times 21-\frac{2}{3} \times \frac{22}{7} \times\left(\frac{21}{2}\right) \times\left(\frac{21}{2}\right) \times\left(\frac{21}{2}\right)$

$=21 \times 21 \times 21 \times\left(1-\frac{2}{3} \times \frac{22}{7} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\right)$

$=21 \times 21 \times 21 \times\left(\frac{1}{1}-\frac{11}{42}\right)$

$=21 \times 21 \times 21 \times\left(\frac{42-11}{42}\right)$

$=21 \times 21 \times\left(\frac{31}{2}\right)$

$=6835.5 \mathrm{~cm}^{3}$