Question:
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
Solution:
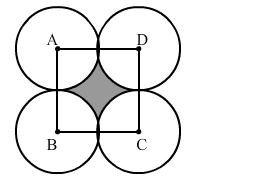
Radius = 5 cm
AB = BC = CD = AD = 10 cm
All sides are equal, so it is a square.
Area of a square $=\mathrm{Side}^{2}$
Area of the square $=10^{2}=100 \mathrm{~cm}^{2}$
Area of the quadrant of one circle $=\frac{1}{4} \pi r^{2}$
$=\frac{1}{4} \times \frac{22}{7} \times 5 \times 5$
$=19.64 \mathrm{~cm}^{2}$
Area of the quadrants of four circles $=19.64 \times 4=78.57 \mathrm{~cm}^{2}$
Area of the shaded portion = Area of the square - Area of the quadrants of four circles
$=100-78.57$
$=21.43 \mathrm{~cm}^{2}$
