Question:
Four equal circles, each of radius 5 cm, touch each other as shown in the following figure. Find the area included between them (Take π = 3.14).
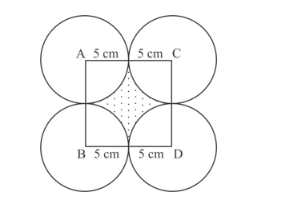
Solution:
It is given that four equal circle touches each other as shown in figure.

Let the side of square is a.
$a=5+5$
$=10 \mathrm{~cm}$
Area of square $=a^{2}$
$=10 \times 10$
$=100 \mathrm{~cm}^{2}$
We know that
Area of circle of radius $r=\pi r^{2}$
$=3.14 \times 5 \times 5$
$=78.5 \mathrm{~cm}^{2}$
Area of quadrant inside square $=\frac{1}{4} \pi r^{2}$
$=\frac{1}{4} \times 78.5 \mathrm{~cm}^{2}$
Area of shaded region $=$ Area of square $-4 \times$ Area of quadrant
$=100-4 \times \frac{1}{4} \times 78.5$
$=100-78.5$
$=21.5 \mathrm{~cm}^{2}$
