Question:
Four dice are thrown simultaneously and the numbers shown on these dice are recorded in $2 \times 2$ matrices. The probability that such formed matrices have all different entries and are non-singular, is :
Correct Option: , 4
Solution:
$A=\left|\begin{array}{ll}a & b \\ c & d\end{array}\right| \quad|A|=a d-b c$
Total case $=6^{4}$
For non-singular matrix $|\mathrm{A}| \neq 0 \Rightarrow \mathrm{ad}-\mathrm{bc} \neq 0$
$\Rightarrow \mathrm{ad} \neq \mathrm{bc}$
And $a, b, c, d$ are all different numbers in the set $\{1,2,3,4,5,6\}$
Now for ad $=\mathrm{bc}$
(i) $6 \times 1=2 \times 3$
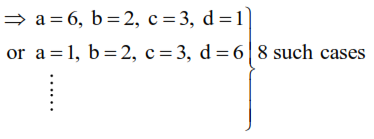
(ii) $6 \times 2=3 \times 4$

favourable cases
$={ }^{6} \mathrm{C}_{4}\lfloor 4-16$
required probability
$=\frac{{ }^{6} \mathrm{C}_{4}\lfloor 4-16}{6^{4}}=\frac{43}{162}$
