Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area.

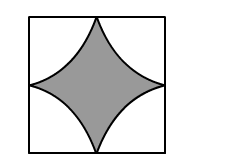
Each cow can graze a region that cannot be accessed by other cows.

$\therefore$ Radius of the region grazed by each cow $=\frac{50}{2}=25 \mathrm{~m}$

Area that each cow grazes $=\frac{1}{4} \times \pi \times r^{2}$

$=\frac{1}{4} \times 3.14 \times 25 \times 25$

$=490.625 \mathrm{~cm}^{2}$

Total area grazed $=4 \times 490.625=1963.49 \mathrm{~m}^{2}$

Area of the square $=(\text { Side })^{2}$

$=50^{2}$

$=2500 \mathrm{~cm}^{2}$

Now,

Area left ungrazed = Area of the square $-$ Grazed area

$=2500-1963.49=536.51 \mathrm{~m}^{2}$