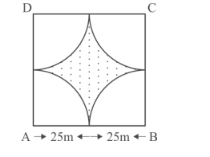
Four cows are tethered at four corners of a square plot of side 50 m,

It is given that four cows are tethered at four corner of square ABCD. We have to find the area of plot that will left ungrazed.

Let the side of square is a.

a = 25 + 25 m = 50 m

Area of square $=a^{2}$

$=50 \times 50$

$=2500 m^{2}$

Area of quadrant inside square $=\frac{1}{4} \pi r^{2}$

$=\frac{1}{4} \times \frac{22}{7} \times 25 \times 25$

$=491.07 \mathrm{~m}^{2}$

Area of shaded region $=$ Area of square $-4 \times$ Area of quadrant

$=2500-4 \times 491.07$

$=2500-1964.28$

$=535.71 \mathrm{~m}^{2}$