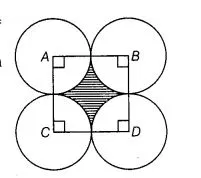
Four circular cardboard pieces of radii 7 cm

Given that, four circular cardboard pieces arc placed on a paper in such a way that each piece touches other two pieces.

Now, we join centre of all four circles to each other by a line segment. Since, radius of each circle is 7 cm.

So,           AB = 2 x Radius of circle

= 2×7 = 14cm

⇒             AB = BC = CD = AD = 14cm

which shows that, quadrilateral $A B C D$ is a square with each of its side is $14 \mathrm{~cm}$.

We know that, each angle between two adjacent sides of a square is $90^{\circ}$.

$\therefore$ Area of sector with $\angle A=90^{\circ}$.

$=\frac{\angle A}{360^{\circ}} \times \pi r^{2}=\frac{90^{\circ}}{360^{\circ}} \times \pi \times(7)^{2}$

$=\frac{1}{4} \times \frac{22}{7} \times 49=\frac{154}{4}=\frac{77}{2}$

$=38.5 \mathrm{~cm}^{2}$

$\therefore \quad$ Area of each sector $=4 \times$ Area of sector with $\angle \mathrm{A}$

$=4 \times 38.5$

$=154 \mathrm{~cm}^{2}$

and area of square $A B C D=(\text { side of square })^{2}$

$=(14)^{2}=196 \mathrm{~cm}^{2} \quad\left[\therefore\right.$ area of square $\left.=(\text { side })^{2}\right]$

So, area of shaded region enclosed between these pieces $=$ Area of square $A B C D$

- Area of each sector

$=196-154$

$=42 \mathrm{~cm}^{2}$

Hence, required area of the portion enclosed between these pieces is 42 cm2.