For what value of k, is −2 a zero of the polynomial 3x2 + 4x + 2k?

We know that if $x=\alpha$ is zero polynomial then $x-\alpha$ is a factor of $f(x)$

Since $-2$ is a factor of $f(x)$. Therefore $x+2$ is a factor of $f(x)$

Now, we divide $f(x)=3 x^{2}+4 x+2 k$ by $g(x)=x+2$ to find the value of $k$

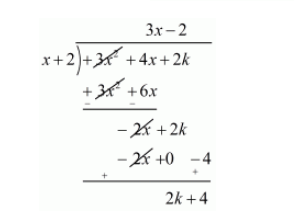
Now, Remainder $=0$

$2 k+4=0$

$2 k=-4$

$k=\frac{-4}{2}$

$k=-2$

Hence, the value of $k$ is $-2$