For the reaction, $a A+b B \rightarrow c C+d D$, the plot of $\log \mathrm{k} \mathrm{vs} \frac{1}{\mathrm{~T}}$ is given below :
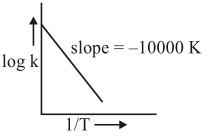
The temperature at which the rate constant of the reaction is $10^{-4} \mathrm{~s}^{-1}$ is __________$\mathrm{K}$. (Rounded-off to the nearest integer) [Given : The rate constant of the reaction is $10^{-5} \mathrm{~s}^{-1}$ at $500 \mathrm{~K}$.]
$\log \mathrm{K}=\log \mathrm{A}-\frac{\mathrm{Ea}}{2.303 \mathrm{RT}}$
$\mid$ Slope $\mid=\frac{\mathrm{Ea}}{2.303 \mathrm{R}}=10,000$
$\log \left(\frac{\mathrm{K}_{2}}{\mathrm{~K}_{1}}\right)=\frac{\mathrm{Ea}}{2.303 \mathrm{R}}\left(\frac{1}{\mathrm{~T}_{1}}-\frac{1}{\mathrm{~T}_{2}}\right)$
$\log \left(\frac{10^{-4}}{10^{-5}}\right)=10,000\left[\frac{1}{500}-\frac{1}{\mathrm{~T}_{2}}\right]$
$\mathrm{T}_{2}=526.31 \simeq 526 \mathrm{~K}$
Hence answer is
$(526)$
