Question:
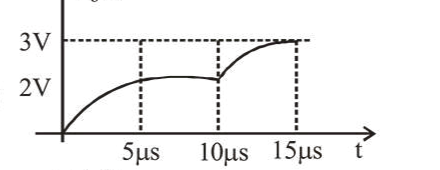
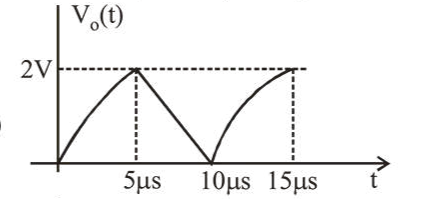
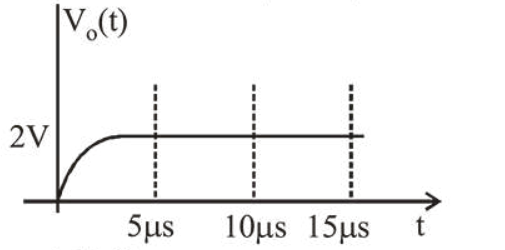
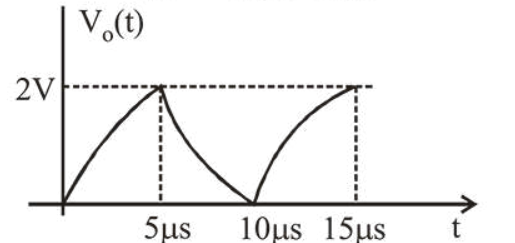
For the given input voltage waveform $V_{\text {in }}(t)$, the output voltage waveform $\mathrm{V}_{0}(t)$, across the capacitor is correctly depicted by:
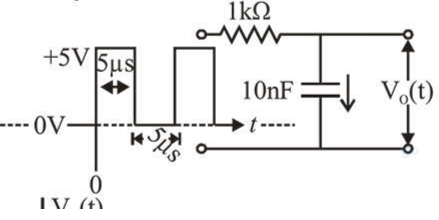
Correct Option: 1,
Solution:
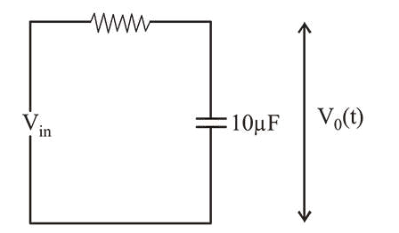
(1) When first pulse is applied, the potential across capacitor
$V_{0}(t)=V_{\text {in }}\left(1-e^{\frac{1}{R C}}\right)$
At $t=5 \mu s=5 \times 10^{-6} s$
$V_{0}(t)=5\left(1-e^{\frac{5 \times 10^{-6}}{10^{3} \times 10 \times 10^{-9}}}\right)=5\left(1-e^{-0.5}\right)=2 V$
When no pulse is applied, capacitor will discharge.
Now, $V_{\text {in }}=0$ means discharging.
$V_{0}(t)=2 e^{\frac{1}{R C}}=2 e^{-0.5}=1.21 \mathrm{~V}$
Now for next $5 \mu \mathrm{s}$