For the following distribution, calculate mean using all suitable methods:

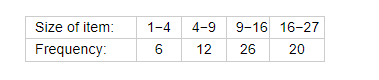
Solution:

Direct Method:

We may prepare the table as shown:

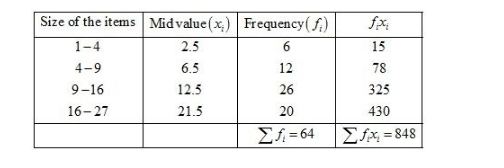
We know that mean, $\bar{X}=\frac{\sum f_{i} x_{i}}{\sum f_{i}}$

$=\frac{848}{64}$

 

$=13.25$

Hence, the mean is 13.25.

Short-Cut Method:

We may prepare the table as shown:

Let the assumed mean be A = 12.5.

We know that mean, $\bar{X}=A+\frac{\sum f_{1} d_{1}}{\sum f_{1}}$

$=12.5+\frac{48}{64}$

$=12.5+0.75$

 

$=13.25$

Hence, the mean is 13.25.

Step-deviation method cannot be used to evaluate the mean of the distribution as the width of the class intervals are not equal. Here, h is not fixed.