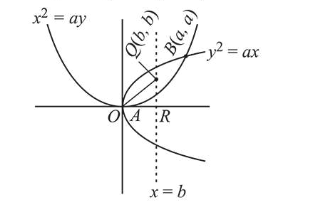
For $a>0$, let the curves $C_{1}: y^{2}=a x$ and $C_{2}: x^{2}=a y$ intersect at origin $O$ and a point $P$. Let the line $x=b(0 the curves, $C_{1}$ and $C_{2}$, and the area of $\Delta O Q R=\frac{1}{2}$, then ' $a$ ' satisfies the equation:
Correct Option: , 2
Given eqns. are, $x^{2}=a y$ and $y^{2}=a x$
After solving, we get $x=a, y=a$
Now, coordinates of $B$ is $(a, a)$ and $A$ is $(0,0)$
Now, coordinates of $Q$ is $(b, b)$
$\therefore \quad \frac{1}{2} b^{2}=\frac{1}{2} \quad \Rightarrow \quad b=1$
Area bounded by curves and $x=1$ is
$\int_{0}^{1}\left(\sqrt{a} x^{1 / 2}-\frac{x^{2}}{a}\right) d x=\frac{1}{2} \int_{0}^{a}\left(\sqrt{a} x^{1 / 2}-\frac{x^{2}}{a}\right) d x$
$\Rightarrow \quad \frac{2}{3} \sqrt{a}-\frac{1}{3 a}=\frac{a^{2}}{6}$
$\Rightarrow \quad 4 a \sqrt{a}-2=a^{3}$
$\Rightarrow \quad a^{6}+4 a^{3}+4=16 a^{3}$
$\Rightarrow \quad a^{6}-12 a^{3}+4=0$
