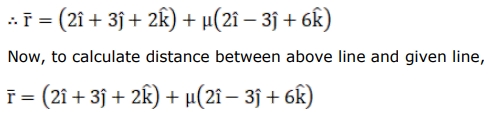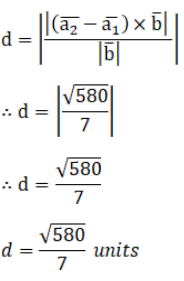Question:
Find the vector equation of a line passing through the point $(2,3,2)$ and parallel to the line
$\vec{r}=(-2 \hat{i}+3 \hat{j})+\lambda(2 \hat{i}-3 \hat{j}+6 \hat{k})$ Also, find the distance between these lines.
HINT: The given line is
$L_{1}: \vec{r}=(-2 \hat{i}+3 \hat{j})+\lambda(2 \hat{i}-3 \hat{j}+6 \hat{k})$
The required line is
$\mathrm{L}_{2}: \overrightarrow{\mathrm{r}}=(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}})+\mu(2 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}+6 \hat{\mathrm{k}})$
Now, find the distance between the parallel lines $L_{1}$ and $L_{2}$.
Solution: