Find the value of k so that the lines

Solution:

Given that $3 x-y-2=0$,

$5 x+k y-3=0$

and $2 x+y-3=0$ are concurrent

We know that,

The lines $a_{1} x+b_{1} y+c_{1}=0, a_{1} x+b_{1} y+c_{1}=0$ and $a_{1} x+b_{1} y+c_{1}=0$ are concurrent if

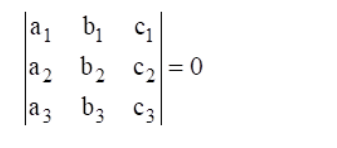
It is given that the given lines are concurrent.

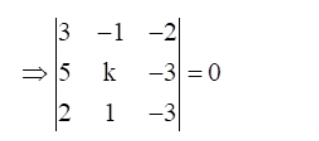
Now, expanding along first row, we get

$\Rightarrow 3[(k)(-3)-(-3)(1)]-(-1)[(5)(-3)-(-3)(2)]+(-2)[5-2 k]=0$

$\Rightarrow 3[-3 k+3]+1[-15+6]-2[5-2 k]=0$

$\Rightarrow-9 k+9-9-10+4 k=0$

$\Rightarrow-5 k-10=0$

$\Rightarrow-5 k=10$

$\Rightarrow k=-2$

Hence, the value of k = -2