Find the squares of the following numbers using column method.

(i) Here, a = 2, b = 5

Step 1. Make 3 columns and write the values of a2, 2 x a x b, and b2 in these columns.

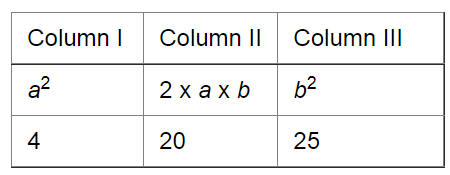
Step 2. Underline the unit digit of b2 (in Column III) and add its tens digit, if any, with 2 x a x b (in Column II).

Step 3. Underline the unit digit in Column II and add the number formed by the tens and other digits, if any, with a2 in Column I.

Step 4. Underline the number in Column I.

Step 5. Write the underlined digits at the bottom of each column to obtain the square of the given number.

In this case, we have:

252 = 625

Using multiplication:

25

$\frac{25}{125}$

$\frac{50}{625}$

This matches with the result obtained by the column method.

(ii) Here, a = 3, b = 7

Step 1. Make 3 columns and write the values of a2, 2 x a x b, and b2 in these columns.

Step 2. Underline the unit digit of b2 (in Column III) and add its tens digit, if any, with 2 x a x b (in Column II).

Step 3. Underline the unit digit in Column II and add the number formed by the tens and other digits, if any, with a2 in Column I.

Step 4. Underline the number in Column I.

Step 5. Write the underlined digits at the bottom of each column to obtain the square of the given number.

In this case, we have:

372 = 1369

Using multiplication:

37

$\frac{37}{259}$

$\frac{111}{1369}$

This matches with the result obtained using the column method.

(iii) Here, a = 5, b = 4

Step 1. Make 3 columns and write the values of a2, 2 x a x b and b2 in these columns.

Step 2. Underline the unit digit of b2 (in Column III) and add its tens digit, if any, with 2 x a x b (in Column II).

Step 3. Underline the unit digit in Column II and add the number formed by the tens and other digits, if any, with a2 in Column I.

Step 4. Underline the number in Column I.

Step 5. Write the underlined digits at the bottom of each column to obtain the square of the given number.

In this case, we have:

542 = 2916

Using multiplication:

54

$\frac{54}{216}$

$\frac{270}{2916}$

This matches with the result obtained using the column method.

(iv) Here, a = 7, b = 1

Step 1. Make 3 columns and write the values of a2, 2 x a x b and b2 in these columns.

Step 2. Underline the unit digit of b2 (in Column III) and add its tens digit, if any, with 2 x a x b (in Column II).

Step 3. Underline the unit digit in Column II and add the number formed by the tens and other digits, if any, with a2 in Column I.

Step 4. Underline the number in Column I.

Step 5. Write the underlined digits at the bottom of each column to obtain the square of the given number.

In this case, we have:

712 = 5041

Using multiplication:

71

$\frac{71}{71}$

$\frac{497}{5041}$

This matches with the result obtained using the column method.

(v) Here, a = 9, b = 6

Step 1. Make 3 columns and write the values of a2, 2 x a x b and b2 in these columns.

Step 2. Underline the unit digit of b2 (in Column III) and add its tens digit, if any, with 2 x a x b (in Column II).

Step 3. Underline the unit digit in Column II and add the number formed by the tens and other digits, if any, with a2 in Column I.

Step 4. Underline the number in Column I.

Step 5. Write the underlined digits at the bottom of each column to obtain the square of the given number.

In this case, we have:

962 = 9216

Using multiplication:

96

$\frac{96}{576}$

$\frac{864}{9216}$

This matches with the result obtained using the column method.