Find the missing frequencies in the following

Solution:

We have to find the missing term of the following distribution table if $N=100$ and median is 32 .

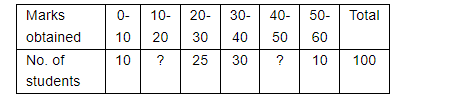
Suppose the missing term are x and y.

Now we have to find the cumulative frequency as

From the above distribution median class is 30-40 and

$l=30$

$N=100$

$h=10$

$f=30$

$C=35+x$

Therefore,

$N=100=75+x+y$

$\Rightarrow x+y=25$.........(1)

Now we are using the following relation

median $=l+\frac{\frac{N}{2}-C}{f} \times h$

$\Rightarrow 32=30+\frac{\frac{100}{2}-(35+x)}{30} \times 10$

$\Rightarrow 96=90+50-35-x$

$\Rightarrow x=9$

Now we are putting the value of x in the equation (1), we get

$9+y=25$

$\Rightarrow y=16$

Hence the missing terms are