Question:
Find the mean deviation about median for the following data:
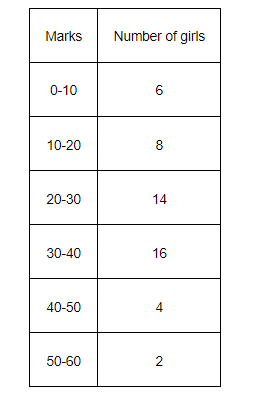
Solution:
The following table is formed.
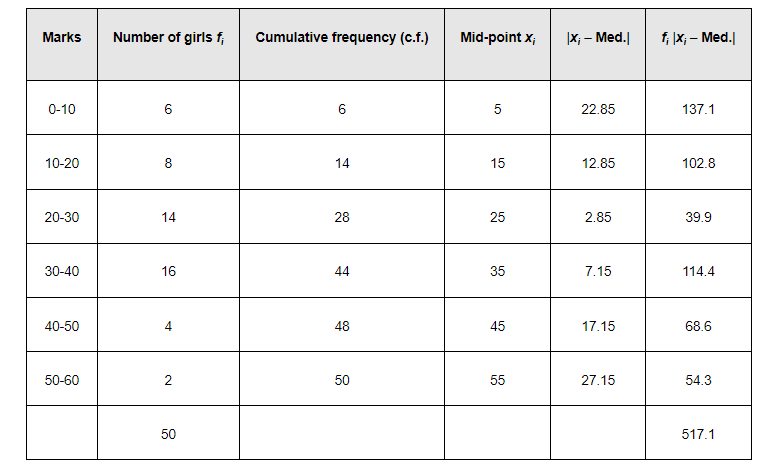
The class interval containing the $\left(\frac{\mathrm{N}}{2}\right)$ or $25^{\text {th }}$ item is $20-30$.
Therefore, 20 – 30 is the median class.
It is known that,
Median $=l+\frac{\frac{\mathrm{N}}{2}-\mathrm{C}}{f} \times h$
Here, $I=20, C=14, f=14, h=10$, and $N=50$
$\therefore$ Median $=20+\frac{25-14}{14} \times 10=20+\frac{110}{14}=20+7.85=27.85$
Thus, mean deviation about the median is given by,
M.D. $(\mathrm{M})=\frac{1}{\mathrm{~N}} \sum_{i=1}^{0} f_{i}\left|x_{i}-\mathrm{M}\right|=\frac{1}{50} \times 517.1=10.34$
