Find the mean and variance of the frequency

Given the frequency distribution

Now we have to find the mean and variance

Converting the ranges of x to groups, the given table can be rewritten as shown below,

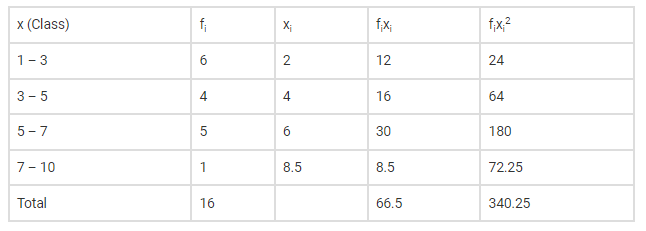
And we know variance can be written as

$\sigma^{2}=\frac{\sum f_{i} x_{i}^{2}}{n}-\left(\frac{\sum f_{i} x_{i}}{n}\right)^{2}$

Substituting values from above table, we get

$\sigma^{2}=\frac{340.25}{16}-\left(\frac{66.5}{16}\right)^{2}$

On simplifying we get

$\sigma^{2}=21.265-(4.16)^{2}$

$\sigma^{2}=21.265-17.305=3.96$

We also know mean can be written as

$\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}$

Substituting values from above table, we get

$\bar{x}=\frac{66.5}{16}=4.16$

Hence the mean and variance of the given frequency distribution is $4.16$ and $3.96$ respectively.