Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long.

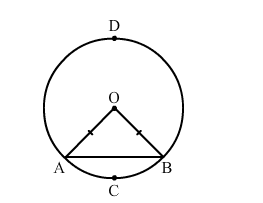
Let AB be the chord. Joining A and B to O, we get an equilateral triangle OAB.
Thus, we have:

$\angle O=\angle A=\angle B=60^{\circ}$

Length of the arc ACB:

$2 \pi \times 12 \times \frac{60}{360}$

$=4 \pi$

$=12.56 \mathrm{~cm}$

Length of the arc ADB:

Circumference of the circle - Length of the arc ACB

$=2 \pi \times 12-4 \pi$

$=20 \pi \mathrm{cm}$

$=62.80 \mathrm{~cm}$

Now,
Area of the minor segment:

Area of the sector - Area of the triangle

$=\left[\pi \times(12)^{2} \times \frac{60}{360}-\frac{\sqrt{3}}{4} \times(12)^{2}\right]$

$=13.08 \mathrm{~cm}^{2}$