Find the length of the perpendicular from the origin to each of the following lines :

Given: Point (0,0) and line 7x + 24y = 50

To find: The length of the perpendicular from the origin to the line $7 x+24 y=50$

Formula used:

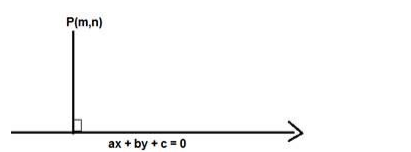
We know that the length of the perpendicular from P (m,n) to the line ax + by + c = 0 is given by,

$D=\frac{|a m+b n+c|}{\sqrt{a^{2}+b^{2}}}$

The given equation of the line is $7 x+24 y-50=0$

Here $m=0$ and $n=0, a=7, b=24, c=-50$

$D=\frac{|7(0)+24(0)-50|}{\sqrt{7^{2}+24^{2}}}$

$D=\frac{|0+0-50|}{\sqrt{49+576}}=\frac{|-50|}{\sqrt{625}}=\frac{|-50|}{25}=\frac{50}{25}=2$

D = 2

The length of perpendicular from the origin to the line $7 x+24 y=50$ is 2 units

(ii) Given: Point (0,0) and line 4x + 3y = 9

To find: The length of perpendicular from the origin to the line 4x + 3y = 9

Formula used:

We know that the length of perpendicular from P (m,n) to the line ax + by + c = 0 is given by

$D=\frac{|a m+b n+c|}{\sqrt{a^{2}+b^{2}}}$

The given equation of the line is $4 x+3 y-9=0$

Here $m=0$ and $n=0, a=4, b=3, c=-9$

$D=\frac{|4(0)+3(0)-9|}{\sqrt{4^{2}+3^{2}}}$

$D=\frac{|0+0-9|}{\sqrt{16+9}}=\frac{|-9|}{\sqrt{25}}=\frac{|-9|}{5}=\frac{9}{5}$

$D=\frac{9}{5}$

The length of perpendicular from the origin to the line $4 x+3 y=9$ is $\frac{9}{5}$ units

(iii) Given: Point (0,0) and line x = 4

To find: The length of perpendicular from the origin to the line x = 4

Formula used: We know that the length of perpendicular from $(\mathrm{m}, \mathrm{n})$ to the line $\mathrm{ax}+\mathrm{by}$ $+c=0$ is given by,

$D=\frac{|a m+b n+c|}{\sqrt{a^{2}+b^{2}}}$

$D=\frac{|a m+b n+c|}{\sqrt{a^{2}+b^{2}}}$

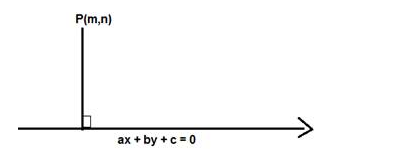
The given equation of the line is $x-4=0$

Here $m=0$ and $n=0, a=1, b=0, c=-4$

$D=\frac{|1(0)+0(0)-4|}{\sqrt{1^{2}+0^{2}}}$

$D=\frac{|0+0-4|}{\sqrt{1+0}}=\frac{|-4|}{\sqrt{1}}=\frac{|-4|}{1}=4$

$D=4$

The length of perpendicular from the origin to the line x = 4 is 4 units