Find the following product:

To find the product, we will use the distributive law in the following way:

$-\frac{8}{27} x y z\left(\frac{3}{2} x y z^{2}-\frac{9}{4} x y^{2} z^{3}\right)$

$=\left\{\left(-\frac{8}{27} x y z\right)\left(\frac{3}{2} x y z^{2}\right)\right\}-\left\{\left(-\frac{8}{27} x y z\right)\left(\frac{9}{4} x y^{2} z^{3}\right)\right\}$

$=\left\{\left(-\frac{8}{27} \times \frac{3}{2}\right)(x \times x) \times(y \times y) \times\left(z \times z^{2}\right)\right\}-\left\{\left(-\frac{8}{27} \times \frac{9}{4}\right)(x \times x) \times\left(y \times y^{2}\right) \times\left(z \times z^{3}\right)\right\}$

$=\left\{\left(-\frac{8}{27} \times \frac{3}{2}\right)\left(x^{1+1} y^{1+1} z^{1+2}\right)\right\}-\left\{\left(-\frac{8}{27} \times \frac{9}{4}\right)\left(x^{1+1} y^{1+2} z^{1+3}\right)\right\}$

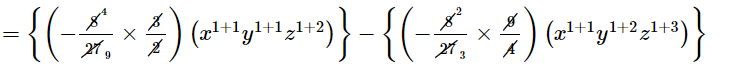
$=-\frac{4}{9} x^{2} y^{2} z^{3}+\frac{2}{3} x^{2} y^{3} z^{4}$

Thus, the answer is $-\frac{4}{9} x^{2} y^{2} z^{3}+\frac{2}{3} x^{2} y^{3} z^{4}$.