Find the equation of the normals to the curve

The equation of the given curve is $y=x^{3}+2 x+6$.

The slope of the tangent to the given curve at any point (x, y) is given by,

$\frac{d y}{d x}=3 x^{2}+2$

∴ Slope of the normal to the given curve at any point (x, y) =

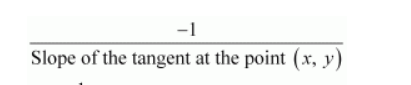
$=\frac{-1}{3 x^{2}+2}$

The equation of the given line is x + 14y + 4 = 0.

$x+14 y+4=0 \Rightarrow y=-\frac{1}{14} x-\frac{4}{14}($ which is of the form $y=m x+c)$

If the normal is parallel to the line, then we must have the slope of the normal being equal to the slope of the line.

$\therefore \frac{-1}{3 x^{2}+2}=\frac{-1}{14}$

$\Rightarrow 3 x^{2}+2=14$

$\Rightarrow 3 x^{2}=12$

$\Rightarrow x^{2}=4$

$\Rightarrow x=\pm 2$

When x = 2, y = 8 + 4 + 6 = 18.

When x = −2, y = − 8 − 4 + 6 = −6.

Therefore, there are two normals to the given curve with slope $\frac{-1}{14}$ and passing through the points $(2,18)$ and $(-2,-6)$.

Thus, the equation of the normal through (2, 18) is given by,

$y-18=\frac{-1}{14}(x-2)$

$\Rightarrow 14 y-252=-x+2$

$\Rightarrow x+14 y-254=0$

And, the equation of the normal through (−2, −6) is given by,

$y-(-6)=\frac{-1}{14}[x-(-2)]$

$\Rightarrow y+6=\frac{-1}{14}(x+2)$

$\Rightarrow 14 y+84=-x-2$

$\Rightarrow x+14 y+86=0$

Hence, the equations of the normals to the given curve (which are parallel to the given line) are $x+14 y-254=0$ and $x+14 y+86=0$.