Find the equation of the line passing through the point (0, 3) and

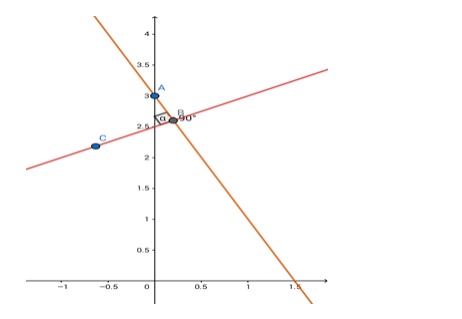
Given: The given line is $x-2 y+5=0$. The line perpendicular to this given line passes through $(0,3)$

Formula to be used: The product of slopes of two perpendicular lines = - 1.

The slope of this line is 1/2 .

$\therefore$ the slope of the perpendicular line $=\frac{-1}{1 / 2}=-2$.

The equation of the line can be written in the form $y=(-2) x+c$

(c is the y - intercept)

This line passes through (0,3) so the point will satisfy the equation of the line.

$\therefore 3=(-2) \times 0+c$ i.e. $c=3$

The required equation is y = - 2x + 3

i.e. 2x + y = 3