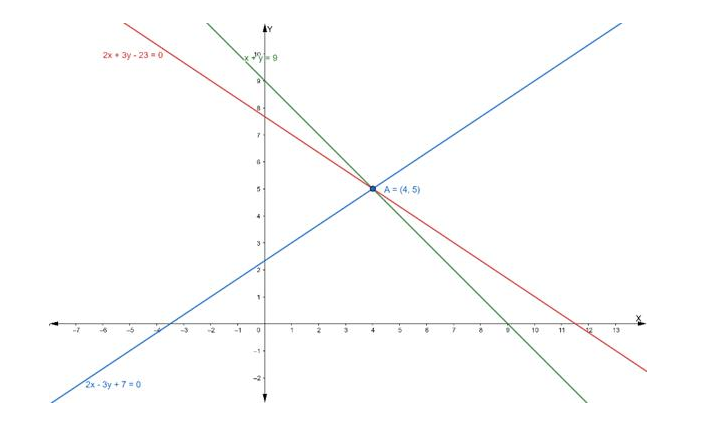
Find the equation of the line drawn through the point of intersection of the

Suppose the given two lines intersect at a point $P\left(x_{1}, y_{1}\right)$. Then, $\left(x_{1}, y_{1}\right)$ satisfies each of the given equations.

$x+y=9 \ldots$ (i)

$2 x-3 y+7=0 \ldots$ (ii)

Now, we find the point of intersection of eq. (i) and (ii)

Multiply the eq. (i) by 2, we get

$2 x+2 y=18$

or $2 x+2 y-18=0 \ldots$ (iii)

On subtracting eq. (iii) from (ii), we get

$2 x-3 y+7-2 x-2 y+18=0$

$\Rightarrow-5 y+25=0$

$\Rightarrow-5 y=-25$

$\Rightarrow y=5$

Putting the value of y in eq. (i), we get

$x+5=9$

$\Rightarrow x=9-5$

$\Rightarrow x=4$

Hence, the point of intersection $\mathrm{P}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ is $(4,5)$

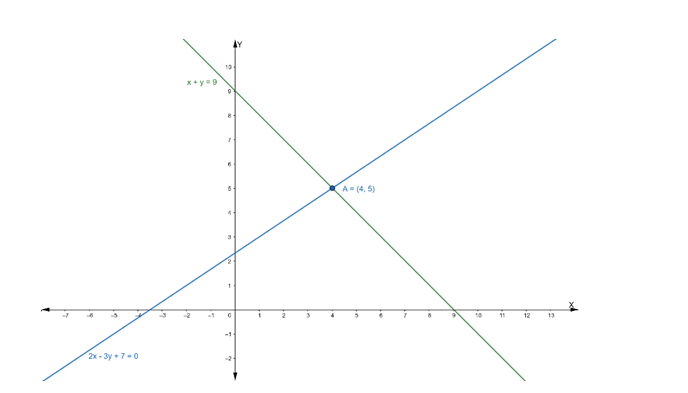
Now, we have to find the equation of the line passing through the point (4, 5) and having

slope $=-\frac{2}{3}$

Equation of line: $y-y_{1}=m\left(x-x_{1}\right)$

$\Rightarrow y-5=-\frac{2}{3}(x-4)$

$\Rightarrow 3 y-15=-2 x+8$

$\Rightarrow 2 x+3 y-15-8=0$

$\Rightarrow 2 x+3 y-23=0$

Hence, the equation of line having slope $-2 / 3$ is $2 x+3 y-23=0$