Find the equation of the line drawn through the point of intersection of the

Suppose the given two lines intersect at a point $P\left(x_{1}, y_{1}\right)$. Then, $\left(x_{1}, y_{1}\right)$ satisfies each of the given equations.

$x-y=1 \ldots(1)$

$2 x-3 y+1=0 \ldots$ (ii)

Now, we find the point of intersection of eq. (i) and (ii)

Multiply the eq. (i) by 2, we get

$2 x-2 y=2$

or $2 x-2 y-2=0 \ldots$ (iii)

On subtracting eq. (iii) from (ii), we get

$2 x-3 y+1-2 x+2 y+2=0$

$\Rightarrow-y+3=0$

$\Rightarrow y=3$

Putting the value of y in eq. (i), we get

$x-3=1$

$\Rightarrow x=1+3$

$\Rightarrow x=4$

Hence, the point of intersection $P\left(x_{1}, y_{1}\right)$ is $(4,3)$

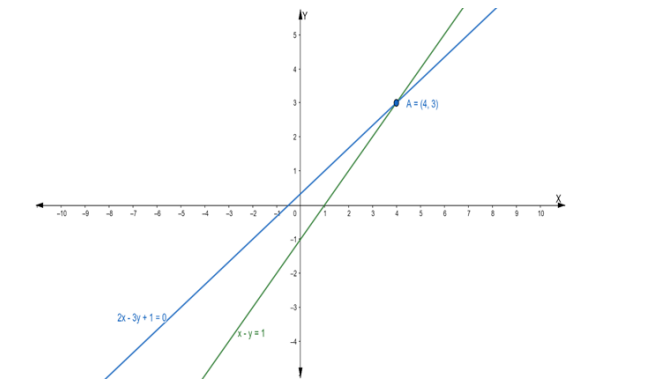
Now, we find the slope of the given equation $3 x+4 y=12$

We know that the slope of an equation is

$\mathrm{m}=-\frac{\mathrm{a}}{\mathrm{b}}$

$\Rightarrow \mathrm{m}=-\frac{3}{4}$

So, the slope of a line which is parallel to this line is also $-\frac{3}{4}$

Then the equation of the line passing through the point $(4,3)$ having a slope $-\frac{3}{4}$ is:

$y-y_{1}=m\left(x-x_{1}\right)$

$\Rightarrow y-(3)=-\frac{3}{4}(x-4)$

$\Rightarrow y-3=-3 x+12$

$\Rightarrow 4 y-12=-3 x+12$

$\Rightarrow 3 x+4 y-12-12=0$

$\Rightarrow 3 x+4 y-24=0$