Find the equation of the ellipse with center at the origin, the major axis on

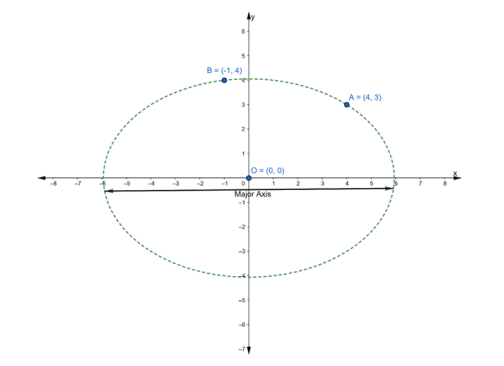
Given: Center is at the origin

and Major axis is along $x$-axis

So, Equation of ellipse is of the form

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ …(i)

Given that ellipse passing through the points $(4,3)$ and $(-1,4)$

So, point $(4,3)$ and $(-1,4)$ will satisfy the eq. (i)

Taking point $(4,3)$ where $x=4$ and $y=3$

Putting the values in eq. (i), we get

$\frac{(4)^{2}}{a^{2}}+\frac{(3)^{2}}{b^{2}}=1$

$\Rightarrow \frac{16}{a^{2}}+\frac{9}{b^{2}}=1$ …(ii)

Taking point $(-1,4)$ where $x=-1$ and $y=4$

Putting the values in eq. (i), we get

$\frac{(-1)^{2}}{a^{2}}+\frac{(4)^{2}}{b^{2}}=1$

$\Rightarrow \frac{1}{a^{2}}+\frac{16}{b^{2}}=1$ …(iii)

Now, we have to solve the above two equations to find the value of $a$ and $b$

Multiply the eq. (iii) by 16 , we get

$\frac{16}{a^{2}}+\frac{16 \times 16}{b^{2}}=1 \times 16$

$\Rightarrow \frac{16}{a^{2}}+\frac{256}{b^{2}}=16$ …(iv)

Subtracting eq. (iv) from (ii), we get

$\Rightarrow \frac{9-256}{\mathrm{~b}^{2}}=-15$

$\Rightarrow-\frac{247}{\mathrm{~b}^{2}}=-15$

$\Rightarrow \mathrm{b}^{2}=\frac{247}{15}$

Substituting the value of $b^{2}$ in eq. (iii), we get

$\frac{1}{a^{2}}+\frac{16}{\frac{247}{15}}=1$

$\Rightarrow \frac{1}{a^{2}}+\frac{15 \times 16}{247}=1$

$\Rightarrow \frac{1}{a^{2}}+\frac{240}{247}=1$

$\Rightarrow \frac{1}{a^{2}}=1-\frac{240}{247}$

$\Rightarrow \frac{1}{a^{2}}=\frac{247-240}{247}$

$\Rightarrow \frac{1}{a^{2}}=\frac{7}{247}$

$\Rightarrow a^{2}=\frac{247}{7}$

Thus

$\mathrm{a}^{2}=\frac{247}{7} \& \mathrm{~b}^{2}=\frac{247}{15}$

Substituting the value of $a^{2}$ and $b^{2}$ in eq. (i), we get

$\frac{x^{2}}{\frac{247}{7}}+\frac{y^{2}}{\frac{247}{15}}=1$

$\Rightarrow \frac{7 x^{2}}{247}+\frac{15 y^{2}}{247}=1$

$\Rightarrow 7 x^{2}+15 y^{2}=247$