Find the equation of the ellipse whose foci are at

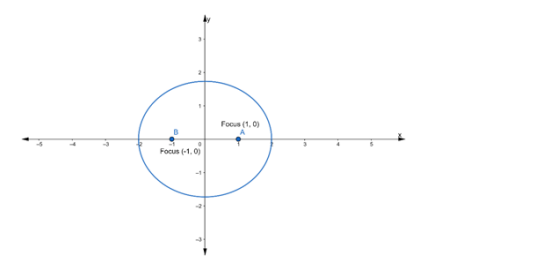
Let the equation of the required ellipse be

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

Given:

Coordinates of foci $=(\pm 1,0) \ldots(\mathrm{i})$

We know that,

Coordinates of foci $=(\pm c, 0) \ldots$ (ii)

$\therefore$ From eq. (i) and (ii), we get

c = 1

It is also given that

Eccentricity $=\frac{1}{2}$

we know that,

Eccentricity, $e=\frac{c}{a}$

$\Rightarrow \frac{1}{2}=\frac{1}{a}[\because c=1]$

$\Rightarrow a=2$

Now, we know that,

$c^{2}=a^{2}-b^{2}$

$\Rightarrow(1)^{2}=(2)^{2}-b^{2}$

$\Rightarrow 1=4-b^{2}$

$\Rightarrow b^{2}=4-1$

$\Rightarrow b^{2}=3$

Substituting the value of $a^{2}$ and $b^{2}$ in the equation of an ellipse, we get

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

$\Rightarrow \frac{x^{2}}{4}+\frac{y^{2}}{3}=1$