Find the equation of the circle whose centre is

Solution:

The general form of the equation of a circle is:

$(x-h)^{2}+(y-k)^{2}=r^{2}$

Where, (h, k) is the centre of the circle.

r is the radius of the circle.

In this question we know that $(h, k)=(2,-5)$, so for determining the equation of the circle we need to determine the radius of the circle.

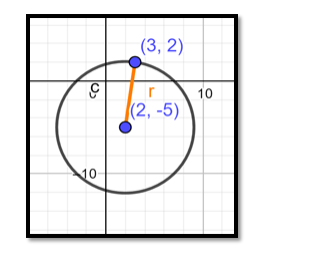
Since the circle passes through $(3,2)$, that pair of values for $x$ and $y$ must satisfy the equation and we have:

$\Rightarrow(3-2)^{2}+(2-(-5))^{2}=r^{2}$

$\Rightarrow 1^{2}+7^{2}=r^{2}$

$\Rightarrow r^{2}=49+1=50$

$\therefore r^{2}=50$

⇒ Equation of circle is:

$(x-2)^{2}+(y-(-5))^{2}=50$

$\Rightarrow(x-2)^{2}+(y+5)^{2}=50$

Ans: $(x-2)^{2}+(y+5)^{2}=50$