Find the equation of the circle whose centre

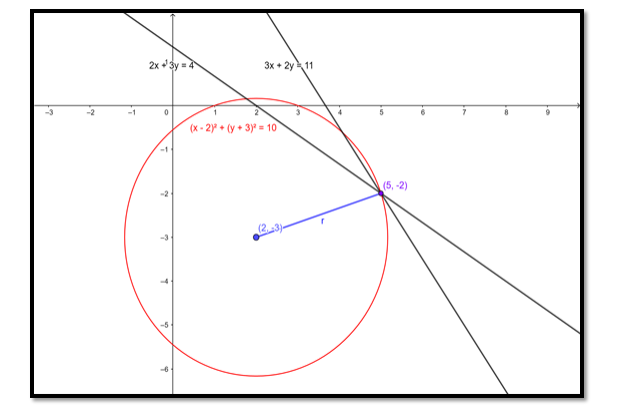
The intersection of the lines: 3x + 2y = 11 and 2x + 3y = 4

Is $(5,-2)$

$\therefore$ This problem is same as solving a circle equation with centre and point on the circle given.

The general form of the equation of a circle is:

$(x-h)^{2}+(y-k)^{2}=r^{2}$

Where, (h, k) is the centre of the circle.

r is the radius of the circle.

In this question we know that $(\mathrm{h}, \mathrm{k})=(2,-3)$, so for determining the equation of the circle we need to determine the radius of the circle.

Since the circle passes through $(5,-2)$, that pair of values for $x$ and $y$ must satisfy the equation and we have:

$\Rightarrow(5-2)^{2}+(-2-(-3))^{2}=r^{2}$

$\Rightarrow 3^{2}+1^{2}=r^{2}$

$\Rightarrow r^{2}=9+1=10$

$\therefore \mathrm{r}^{2}=10$

⇒ Equation of circle is:

$(x-2)^{2}+(y-(-3))^{2}=10$

$\Rightarrow(x-2)^{2}+(y+3)^{2}=10$

Ans: $(x-2)^{2}+(y+5)^{2}=10$