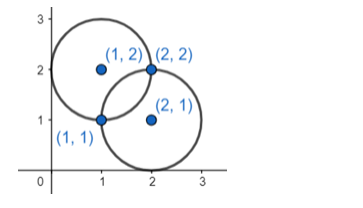
Find the equation of the circle which passes through the points

The general equation of a circle: $(x-h)^{2}+(y-k)^{2}=r^{2}$

$\ldots(\mathrm{i})$, where $(\mathrm{h}, \mathrm{k})$ is the centre and $\mathrm{r}$ is the radius.

Putting $A(1,1)$ in (i)

$(1-h)^{2}+(1-k)^{2}=1^{2}$

$\Rightarrow h^{2}+k^{2}+2-2 h-2 k=1$

$\Rightarrow h^{2}+k^{2}-2 h-2 k=-1 . .$ (ii)

Putting $B(2,2)$ in (i)

$(2-h)^{2}+(2-k)^{2}=1^{2}$

$\Rightarrow h^{2}+k^{2}+8-4 h-4 k=1$

$\Rightarrow h^{2}+k^{2}-4 h-4 k=-7$

$\Rightarrow\left(h^{2}+k^{2}-2 h-2 k\right)-2 h-2 k=-7$

$\Rightarrow-1-2 h-2 k=-7[$ from (ii) $]$

$\Rightarrow-2 h-2 k=-6$

$\Rightarrow h+k=3 \Rightarrow h=3-k$

Putting it in (ii)

$\Rightarrow(3-k)^{2}+k^{2}-2(3-k)-2 k=-1$

$\Rightarrow 2 k^{2}+4-6 k=0$

$\Rightarrow k^{2}-3 k+2=0$

$\Rightarrow \mathrm{k}=2$ or $\mathrm{k}=1$

When $k=2, h=3-2=1$

Equation of 1 circle

$(x-1)^{2}+(y-2)^{2}=1$

When $\mathrm{k}=1, \mathrm{~h}=3-1=2$

$(x-2)^{2}+(y-1)^{2}=1$