Find the equation of the circle passing through the points

(i) The required circle equation

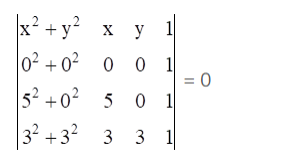
Using Laplace Expansion

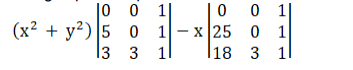
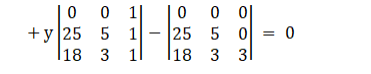
$\Rightarrow 15\left(x^{2}+y^{2}\right)-75 x-15 y=0$

$\Rightarrow \mathrm{x}^{2}+\mathrm{y}^{2}-5 \mathrm{x}-\mathrm{y}=0$ is the equation with centre $=(2.5,0.5)$

Radius $=\sqrt{g^{2}+f^{2}-c}=\sqrt{\left(-2.5^{2}\right)+(-0.5)^{2}-0}=2.549$

(ii) The required circle equation

Using Laplace Expansion

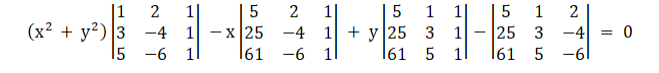
$\Rightarrow 8\left(x^{2}+y^{2}\right)-176 x-32 y-200=0$

$\Rightarrow \mathrm{x}^{2}+\mathrm{y}^{2}-22 \mathrm{x}-4 \mathrm{y}-25=0$ is the equation with centre $=(11,2)$

Radius $=\sqrt{g^{2}+f^{2}-c}=\sqrt{(-11)^{2}+(-2)^{2}-25}=10$

(iii) The required circle equation

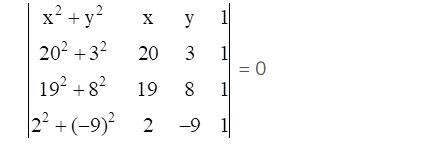
Using Laplace Expansion

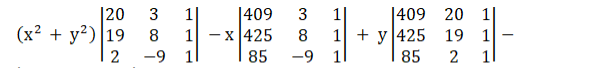
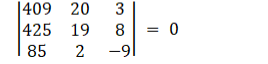
$\Rightarrow 102\left(x^{2}+y^{2}\right)-1428 x-612 y-11322=0$

$\Rightarrow x^{2}+y^{2}-14 x-6 y-111=0$ is the equation with centre = (7, 3)

Radius $=\sqrt{g^{2}+f^{2}-c}=\sqrt{(-7)^{2}+(-3)^{2}-(-111)}=13$