Find the equation of the circle of radius 5 cm

The general form of the equation of a circle is:

$(x-h)^{2}+(y-k)^{2}=r^{2}$

Where, (h, k) is the centre of the circle.

r is the radius of the circle.

Since, centre lies on $Y$-axis, $\therefore$ it's $X$ - coordinate $=0$, i.e.h $=0$

Hence, $(0, k)$ is the centre of the circle.

Substituting the given values in general form of the equation of a circle we get,

$\Rightarrow(3-0)^{2}+(2-k)^{2}=5^{2}$

$\Rightarrow(3)^{2}+(2-k)^{2}=25$

$\Rightarrow 9+(2-k)^{2}=25$

$\Rightarrow(2-k)^{2}=25-9=16$

Taking square root on both sides we get,

$\Rightarrow 2-\mathrm{k}=\pm 4$

$\Rightarrow 2-\mathrm{k}=4 \& 2-\mathrm{k}=-4$

$\Rightarrow \mathrm{k}=2-4 \& \mathrm{k}=2+4$

$\Rightarrow \mathrm{k}=-2 \& \mathrm{k}=6$

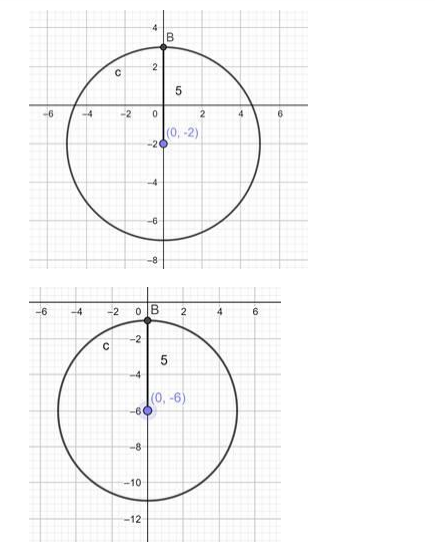
$\therefore$ Equation of circle when $\mathrm{k}=-2$ is: $\mathrm{x}^{2}+(\mathrm{y}+2)^{2}=25$

Equation of circle when $k=6$ is: $x^{2}+(y-6)^{2}=25$

Ans: Equation of circle when $\mathrm{k}=-2$ is:

$x^{2}+(y+2)^{2}=25$

Equation of circle when $k=6$ is: $x^{2}+(y-6)^{2}=25$