Find the equation of the circle concentric with the circle

Solution:

The given image of the circle is:

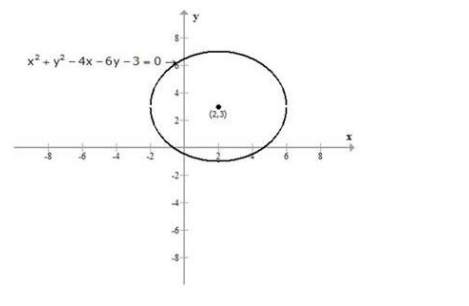
We know that the general equation of the circle is given by:

$x^{2}+y^{2}+2 g x+2 f y+c=0$

Also,

Radius r = $\sqrt{g^{2}+f^{2}-c}$

Now,

$r=\sqrt{(2)^{2}+(3)^{2}-(-3)}$

$r=\sqrt{4+9+3}$

$r=4$ units.

We need to the find the equation of the circle which is concentric to the qiven circle and touches y-axis.

The centre of the circle remains the same.

Now, y-axis will be tangent to the circle.

Point of contact will be $(0,3)$

Therefore, radius $=2$

Now,

Equation of the circle:

$(x-2)^{2}+(y-3)^{2}=(2)^{2}$

$x^{2}+4-4 x+y^{2}+9-6 y=4$

$x^{2}+y^{2}-4 x-6 y+9=0$