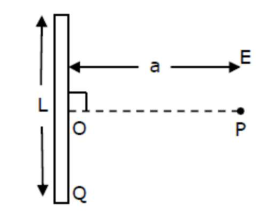
Find the electric field at point $\mathrm{P}$ (as shown in figure) on the perpendicular
bisector of a uniformly charged thin wire of length $\mathrm{L}$ carrying a charge $\mathrm{Q}$.
The distance of the point $\mathrm{P}$ from the centre of the rod is $a=\frac{\sqrt{3}}{2} L$
Correct Option: 1
(1)
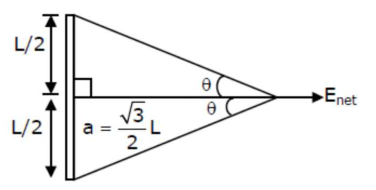
$\tan \theta=\frac{\mathrm{L} / 2}{\frac{\sqrt{3}}{2} \mathrm{~L}} \Rightarrow \frac{1}{\sqrt{3}}$
$\theta=30^{\circ}$
$\mathrm{E}_{\text {net }}=\frac{\mathrm{K} \lambda}{\frac{\sqrt{3}}{2} \mathrm{~L}}\left(\sin 30^{\circ}+\sin 30^{\circ}\right) \Rightarrow \frac{2 \mathrm{KQ}}{\sqrt{3} \mathrm{~L}^{2}}\left(\frac{1}{2}+\frac{1}{2}\right)$
$\mathrm{E}_{\text {net }}=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \mathrm{Q}}{\sqrt{3} L^{2}}$
$\mathrm{E}_{\mathrm{net}}=\frac{\mathrm{Q}}{2 \sqrt{3} \pi \varepsilon_{0} \mathrm{~L}^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.